Computational-intelligence
双中心粒子群优化
1 引言
粒子群优化($PSO$)算法是一种新兴的群体智能优化技术,由于其原理简单、参数少、效果好等 优点已经广泛应用于求解各类复杂优化问题.而影响该算法收敛速度和精度的2个主要因素是粒子个 体极值与全局极值的更新方式.通过分析粒子的飞行轨迹和引入广义中心粒子和狭义中心粒子,提出 双中心粒子群优化($double\; center\; particle\; swarm\; optimization,DCPSO$)算法,在不增加算法复杂度条 件下对粒子的个体极值和全局极值更新方式进行更新,从而改善了算法的收敛速度和精度。
在双中心粒子群优化中,主要有以下改变:
- 改变轨迹探索方式
- 引入广义中心粒子
- 引入狭义中心粒子
2 算法精讲
首先需要明确的是,该算法基本沿用 $A\; Modified\; Particle\; Swarm\; Optimizer$(这里称之为 $OPSO$)中的算法结构,在该结构的基础上进行了三点改变:
- 飞行轨迹搜索改变
- 广义中心粒子
- 狭义中心粒子
因此,只要理解更改的部分便能理解该算法。而这三点改变分别体现在两处,分别是:
- 个体最优位置更新
- 全局最优位置更新
2.1 个体最优位置更新
在 $OPSO$ 中,粒子的更新方式为:
\[v_i^d=\omega v_i^d+c1\times rand_i^d\times (pBest_i^d-x_i^d)+c2\times rand_i^d\times (gBest^d-x_i^d) \tag{1}\]因此,最终位置是通过上面的三项进行合成得到。在双中心粒子群优化中,个体最优位置更新是将上面三项进行拆分,在矢量合成的过程中,会经过三个位置,分别为:
\[x_1 = x + \omega v_i^d\\ x_2 = x_1 + c1\times rand_i^d\times (pBest_i^d-x_i^d)\\ x_3 = x_2 + c2\times rand_i^d\times (gBest^d-x_i^d)\\\]如下图所示:
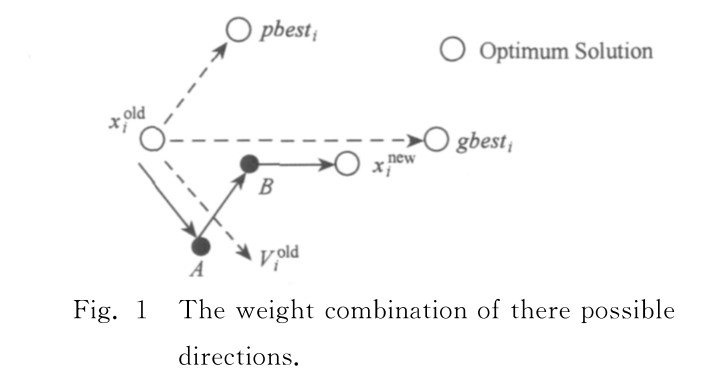
在上图中粒子飞行路径为 $x_{old}\Rightarrow A\Rightarrow B\Rightarrow x_{new}$,就单个粒子而言,折线运动经历的区域比直线方式复 杂,其捕食范围能够被最大程度地覆盖在整个搜索 空间内,体现在$PSO$算法中,每个粒子能够在更为 广阔的搜索空间内寻找最优解,这样粒子的个体极 值就能够得到显著的改善;从粒子群整体来说,每个粒子个体极值的改善将直接影响着种群全局极值的增强,这一影响使得种群能更快地收敛于最优解.
因此在更新时分别会对这三个位置进行比较更新,更新公式如下:
\[f(pBest_i^{new})=min(f(A),f(B),f(x_i^{new},f(pBest_i^{old})))\tag{2}\]注意事项:在个体最优位置更新时需要注意,在更新规则方面论文没有详细描述,通过有限测试,在这几个阶段速度不进行约束,但是位置需要约束,不能超过边界。并且最后要对速度进行归正,即执行公式(1),并且需要对最后的位置进行约束。该方式效果会更好!
- 探讨
其实如果深究,就会发现如果在算法中对速度进行约束,那么肯定就无法得到理想中的三个位置,因为在 $OPSO$ 中更新是整体更新,当速度超出范围就会被限制,但是我们无法知道在哪一处被限制。当然,倘若只对位置进行约束,那的确是不会出现上述现象。但是在参考论文中,速度是有限制的。因此我们无法获得准确的轨迹位置,而是依据上面的思想进行编写!
2.2 全局最优位置更新
在全局位置更新中,双中心粒子群优化引入了广义中心粒子($general center particle,GCP$)及狭义中心粒子($special center particle,SCP$),两者计算公式为:
\(x_d^{GCP}=\frac{1}{n-2}(\sum_{i=1}^{n-2}pBest_{id})\tag{3}\) \(x_d^{SCP}=\frac{1}{n-2}(\sum_{i=1}^{n-2}x_{id})\tag{3}\)
最终全局最优位置更新从所有的历史最优位置以及广义中心粒子、狭义中心粒子中竞选,公式如(4)式:
\[f(gBest)=min(f(pBest_1),f(pBest_2),...,f(pBest_N),f(x^{GCP},f(x^{SCP})))\tag{4}\]3 代码编写
代码详见 $code$ 文件夹!
4 参考文献
[1].汤可宗,柳炳祥,杨静宇,孙廷凯.双中心粒子群优化算法[J].计算机研究与发展,2012,49(05):1086-1094.